To convert odds to probability, take the player's chance of winning, use it as the numerator and divide by the total number of chances, both winning and losing For example, if the odds are 4 to 1, the probability equals 1 / (1 4) = 1/5 or % Odds of 1 to 1 (50%) are called "evens," and a payout of 1 to 1 is called "even money"Negative figures The odds state how much must be bet to win £100 profit eg american odds of 1 would win £100 on a £1 bet Implied Probability Odds correlate to probability eg a 3/1 bet is expected to win one in every 4 attempts, hence the probability is 25% The latest Italy vs Spain odds from William Hill Sportsbook list Italy as 140 favorites (risk $100 to win $140), while the overunder for total goals scored is 25

Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science
Are odds and probability the same
Are odds and probability the same-Probability and Order Versus Evolution BY HENRY M MORRIS, PHD SUNDAY, JULY 01, 1979 One of the strongest direct evidences for special creation is the existence of innumerable highly complex systems in the universe, systems composed of components occurring in a pattern of "order" rather than disorderOf probability, chances and odds are not the same For instance, the odds in favor of A are P(A) / P(Ac) = (3/4)/(1/4) = 3/1 It is said that the odds in favor of A are 31 or that A is an event twice as likely as "not A" Therefore, the odds of A occurring are expressed in the scale of the probability of "A not occurring"




Figure 5 From Ubiquitous Log Odds A Common Representation Of Probability And Frequency Distortion In Perception Action And Cognition Semantic Scholar
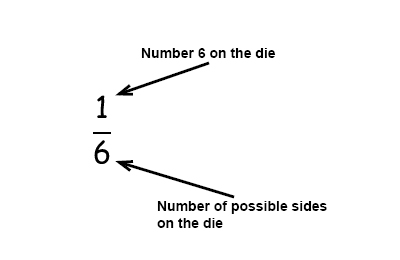
Calculation of probability (risk) vs odds In statistics, odds are an expression of relative probabilities, generally quoted as the odds in favor The odds (in favor) of an event or a proposition is the ratio of the probability that the event will happen to the probability that the event will not happen The Ask Dr Math forum has several entries on odds versus probability Summarizing, one way to conceptualize (nontechnically) the probability of an event is the number of ways that an event can occur divided by the total number of possible outcomes The probability of heads in a fair coin flip is 1/2 (50 percent) Figure 1 The binomial probability distribution function, given 10 tries at p = 5 (top panel), and the binomial likelihood function, given 7 successes in 10 tries (bottom panel) Both panels were computed using the binopdf function In the upper panel, I varied the possible results;
Odds ratio vs probability ratio Ask Question Asked 1 year, 4 months ago Active 3 months ago Viewed 448 times 8 5 $\begingroup$ An odds is the ratio of the probability of an event to its complement $$\text{odds}(X) = \frac{P(X)}{1P(X)}$$ An oddsMany people wrongfully assume odds and probabilities are the same thingThey're definitely not, as there's a significant difference between saying there are Odds Is Related to Probability The formal way to describe the odds is as the probability of the event divided by the probability of the nonevent So odds are the ratio of two fractions the number of events divided by the number of subjects (the probability of the event) and
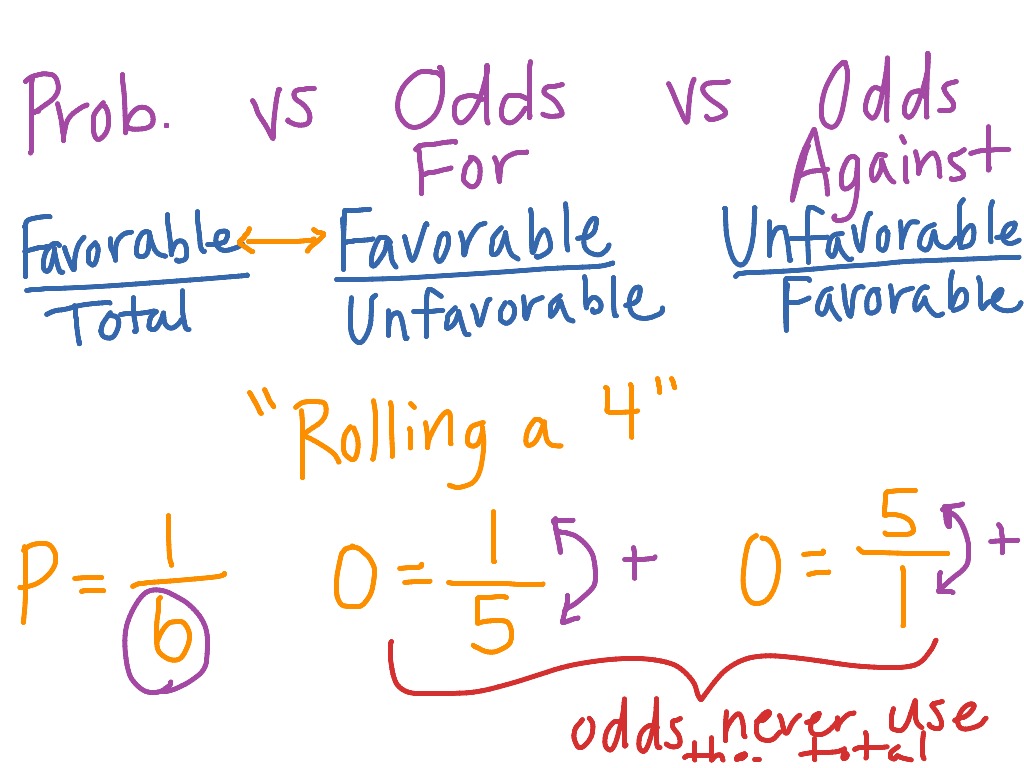
The odds in favor of an event is the ratio of the number of ways the outcome can occur to the number of ways the outcome cannot occur # of ways the event CAN occur # of ways the event CANNOT occur This is actually a lot easier than probability So, let's take a look at an exampleFinding Value In A Moneyline Bet Using an implied probability calculator, you can convert the moneyline odds into an implied chance of winning for each Probability theory is an interesting area of statistics concerned with the odds or chances of an event happening in a trial, eg getting a six when a dice is thrown or drawing an ace of hearts from a pack of cards To work out odds, we also need to have an understanding of permutations and combinations



Ctspedia Ctspedia Oddsterm




What Is An Odds Ratio And How Do I Interpret It Critical Appraisal
A $100 bet would fetch a $100 profit at an implied win probability of 5000% UFC 264 Poirier vs McGregor 3 odds Early prelims Jennifer Maia (0) vs Jessica Eye (160) Maia (1871) gets the edge over Eye (159, 1 NC) in a women's flyweight bout Eye has both the height and reach advantages but has an implied win probability of just 38 Probability compares the number of successes to the total number of attempts made The odds in favor of an event compares the number of successes to the number of failures In what follows, we will see what this means in greater detail First, we consider a little notation The odds are 1626 and probability is 016% If you're playing poker long enough you will somewhat regularly encounter the aces vs kings scenario at a table A formula to estimate the probability for this to happen at a 9 player table is This formula slightly underestimates the actual probability which is a little bit higher




Figure 5 From Ubiquitous Log Odds A Common Representation Of Probability And Frequency Distortion In Perception Action And Cognition Semantic Scholar




Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1
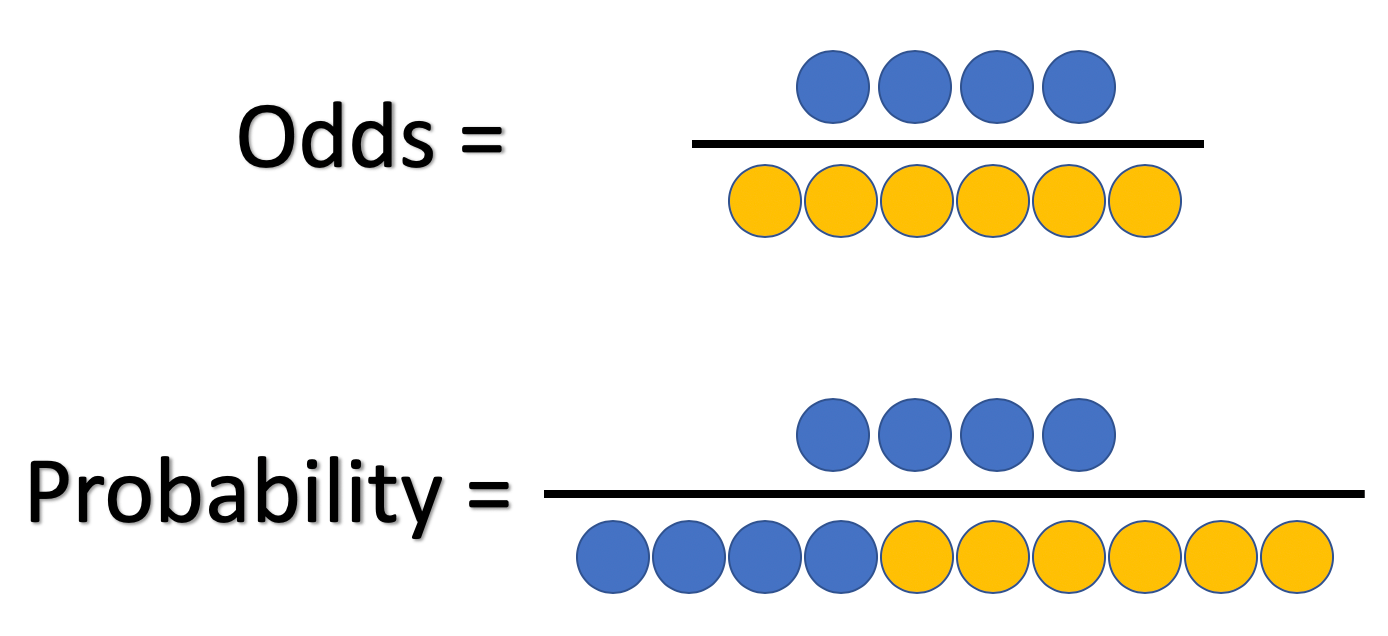
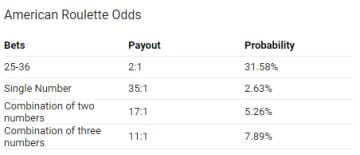
Odds Odds seems less intuitive It is the ratio of the probability a thing will happen over the probability it won't In the spades example, the probability of drawing a spade is 025 The probability of not drawing a spade is 1 025 So the odds is 025/075 or 13 (or 033 or 1/3 pronounced 1 to 3 odds) Moving back and forth Euro Final England vs Italy odds (Cup winner) England 1 (bet $1 to win $100) Italy 110 (bet $110 to win $100) The safer play, as many bettors found out in the semifinals, is to bet the winner of Euro , which can include an extra time result England has implied odds of 5455% to be crowned Euro champion Odds vs Probability Probability is a mathematical assumption of chance that can be calculated using an equation The equation measures the chances for an event to occur against the total number of chances that occurrence may produce




9 2 Binary Logistic Regression R For Health Data Science




Edge Over Odds Demonetized
Odds is a see also of probability As nouns the difference between odds and probability is that odds is the ratio of the probabilities of an event happening to that of it not happening while probability is the state of being probable; Note that the odds for X and odds against X are reciprocals of each other (1/3 is the reciprocal for 3/1), whereas for probabilities, the probability of X and the probability of not X are complements of each other (Thank you, Jeff K Bye, for contributing this note for clarification!) The differences between odds and probability are discussed in the points given below The term 'odds' is used to describe that if there are any chances of the occurrence of an event or not As against, While odds are expressed in the ratio, the probability is either written in percentage form or



Ppt Introduction To Probability Powerpoint Presentation Free Download Id 6021




Probability Stats With Cats Blog
The term 'Odds' is commonplace, but not always clear, and often used inappropriately The odds of an event is the number of events / the number of nonevents This turns out to be equivalent to the probability of an event/the probability of a nonevent You'll often see odds written as P/(1P) Probability Versus Physics The coin toss is not about probability at all, he says It is about physics, the coin, and how the "tosser" is actually throwing it The majority of times, if a coin is headsup when it is flipped, it will remain headsup when it lands Probabilities are usually given as percentages ie 50% probability that a coin will land on HEADS Odds can have any value from zero to infinity and they represent a ratio of desired outcomes versus the field Odds are a ratio, and can be given in two different ways 'odds in favor' and 'odds against'



Introduction To Probability And Statistics




True Odds Calculator Find Probabilities Fair Odds Margin
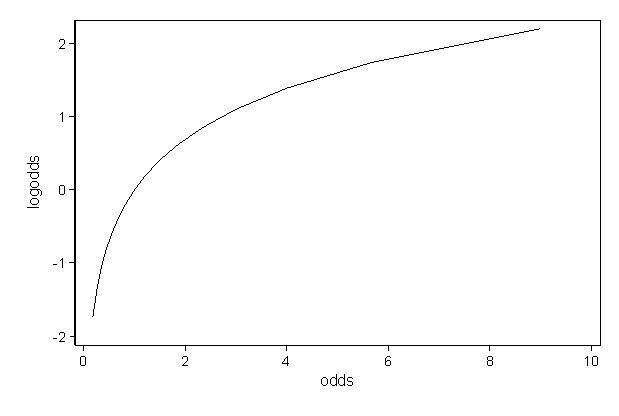
Labs(title ="probability versus odds") 000 025 050 075 100 0 50 100 150 odds p probability versus odds Finally, this is the plot that I think you'llfind most As you can see, the idea of probability is relatively simple But the idea of odds, on the other hand, is a bit more complicatedmostly because there's more than one way to write them The most common way is what's called "bookmakers odds"In the lower, I varied the values of the p parameter The probability distribution function is




Odds Ppt Download



Understanding Uncertainty Visualising Probabilities Plus Maths Org
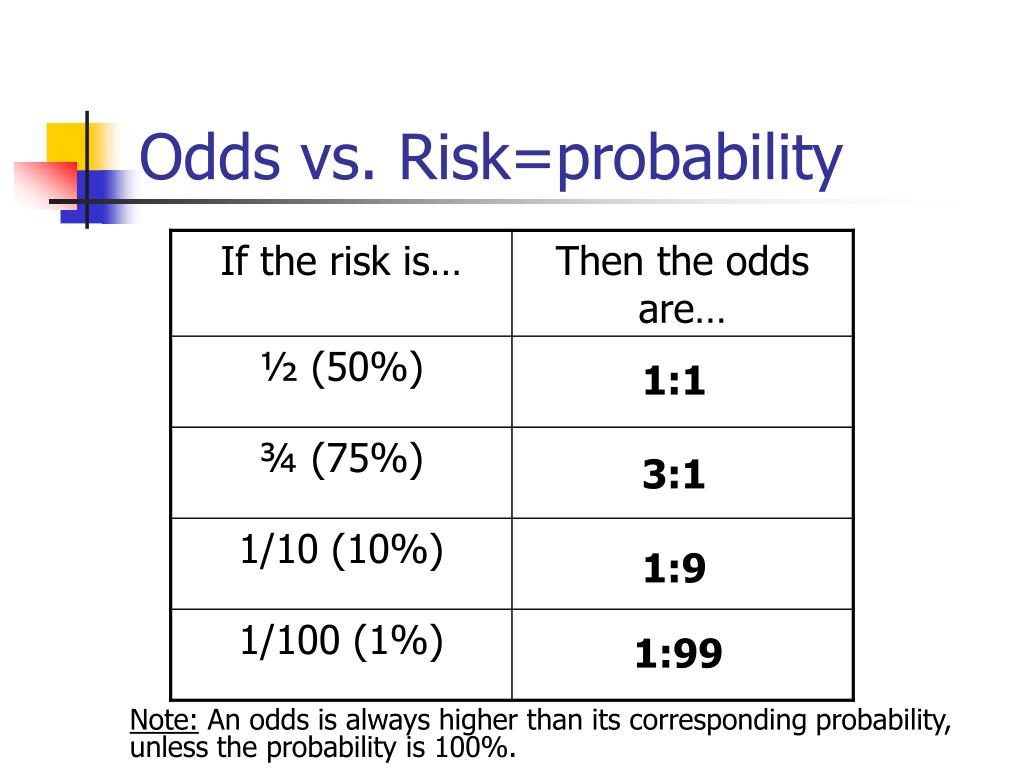
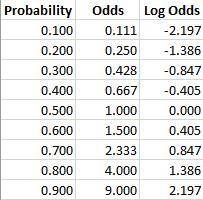
Equal odds are 1 1 success for every 1 failure 11 Equal probabilities are 5 1 success for every 2 trials Odds can range from 0 to infinity Odds greater than 1 indicates success is more likely than failure Odds less than 1 indicates failure is more likely than success Probability can range from 0 to 1 Odds, chances and probability are just different ways of expressing the likelihood of an event In your example of the jackpot that hits on average once per 100,000 spins, the probability of hitting the jackpot is Many people have difficulty relating to a decimal number So another, equivalent way to express the likelihood of hittingIf the probability of success is 5, ie, 5050 percent chance, then the odds of success is 1 to 1 The transformation from probability to odds is a monotonic transformation, meaning the odds increase as the probability increases or vice versa Probability ranges from 0 and 1 Odds range from 0 and positive infinity




Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science




What Is The Difference Between Odds And Probability Statistics Youtube
How to find probability and odds and the difference between the two We also discuss experimental probablility, theoretical probability, odds in favor, and To express odds as a probability, or the other way around, requires a calculation The natural way to interpret odds for (without calculating anything) is as the ratio of events to nonevents in the long run A simple example is that the (statistical) odds for rolling a three with a fair die (one of a pair of dice) are 1 to 5The probability of having the winning plate is 1 out of 25 Odds of winning = number of chances to win number of chances to draw other numbers Odds of winning = 124 (Read as "1 to 24") Odds of not winning = number of chances to draw other numbers number of chances to win Odds of not winning = 241 (Read as "24 to 1")



Proportions Chi Squared Tests And Odds Ratios



What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science
Probability versus Odds A case study While the definitions of these terms can overcomplicate matters, the best way to describe them in action is to look at the coin toss challenge It provides the perfect setting for an explanation of the difference between these two statistical terms because there will only ever be one of two outcomes headsThe chance of winning is 4 out of 52, while the chance against winning is 48 out of 52 (524=48) Entering A=4 and B=48 into the calculator as 448 odds are for winning you get For 4 to 48 odds for winning;This video looks at Odds and Probability through the lens of ratio and proportion which has already been studied at this point Remember the probability for




Odds Ratio The Odds Ratio Is Used To Find The By Analyttica Datalab Medium




Nhanes Tutorials Module 10 Logistic Regression
Probability of Winning = () or % Losing = () or % Odds can be expressed as a ratio of the probability an event will happen divided by the probability an event won't happen Odds in favor of A = A / (1 A), usually simplified to lowest terms, For instance, if the probability of an event occurring is 075, then the odds for it happening are 075/025 = 3/1 = 3 to 1 for, while the probability that it doesn't occur is 1 to 3 againstProbability vs Odds Any chance can be numerically described as either odds or probabilities In the majority of circumstances, neither is preferable to the other The majority of scientists generally refer to probabilities, not odds, but that is more a matter of




Converting Between Probability And Odds Mathwoes Youtube



The Difference Between Probability And Odds
The key is to understand the difference between odds and probability There are 4,655,0 ways you can combine 3odd3even combinations So if you play 3odd3even combination, 33 in every 100 draws will put you in 1 to 46 million advantage rather than 1In this matchup, there is a big difference between the two odds, indicating a much higher probability of Duke winning the game and advancing to the next round of the NCAA Tournament The higher the number, the greater the probability of the outcome Using an example of decimal odds, a candidate has 2 odds to win the next election If so, the implied probability is 4545%
:max_bytes(150000):strip_icc()/dotdash_Final_The_Math_Behind_Betting_Odds_and_Gambling_Nov_2020-01-735accb453c8424b9e063c2c14e4edf4.jpg)



The Math Behind Betting Odds Gambling




Logistic Regression Wikipedia
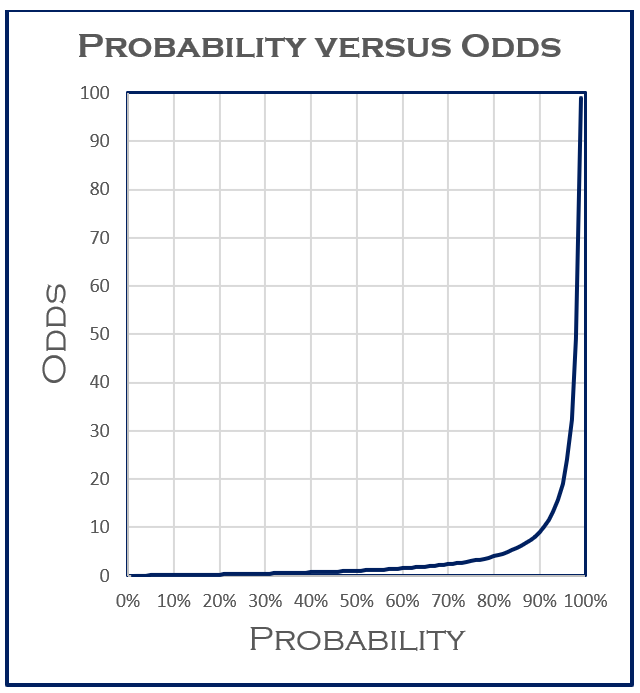
The smaller the probability, the more similar probability and odds will be For example, the probability of winning the UK National Lottery is The odds are The larger the probability, the larger the difference with the odds High probabilities have astronomical odds A probability of 90% equates to odds



Probability Stats With Cats Blog



Relative Risk Ratios And Odds Ratios




Math 30 2 Probability Odds Acceptable Standards 50 79 The Student Can Express Odds For Or Odds Against As A Probability Determine The Probability Ppt Download



Statistics For Medical Students Geeky Medics



Odds Vs Probability Vs Chance Data Science Central




Difference Between Odds And Probability Casinosss




Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios




Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science




Pocket Pair Starting Hands Vs Probability Of Opponent Having A Pocket Pair Poker Stack Exchange



Odds Versus Probability Math Showme




The Difference Between Relative Risk And Odds Ratios The Analysis Factor



Odds Probability The Difference Explained With Examples




What Are The Odds The Annals Of Thoracic Surgery




Implied Probability Betting Math Made Simple 21 Update




Probability Vs Odds In Favour Or Against An Event Examples Youtube



Probability Of Events Pre Algebra Probability And Statistic Mathplanet




How To Calculate Odds 11 Steps With Pictures Wikihow




Calculating The Odds Of An Event Mathematics For The Liberal Arts




Odds Probability And The Lottery Lotterycodex




What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science




Probability



Stanford Edu Class Gene210 Files Lectures 11 4 Salari Analyzinggwasdata Pdf




Odds Ratios And Risk Ratios Youtube




Comparing Probability Odds For And Odds Against Youtube




Estimates Of Odds Ratios Of Daily Probability Of Diarrhea In The Download Scientific Diagram




Likelihood Ratio And Odds Ratio Slope Values Represent Odds As Shown Download Scientific Diagram




Odds Introduction Arbital
:max_bytes(150000):strip_icc()/expected-5733972a5f9b58723d773687.png)



How Odds Are Related To Probability



Log Odds Definition And Worked Statistics Problems



Odds Likelihood Ratios Guide To Diagnostic Tests



Logistic Regression



Converting Between Probability And Odds Mathwoes Youtube




Odds Ratios Versus Relative Risk



1




Probability And Odds Youtube




The Bounded Rationality Of Probability Distortion Pnas
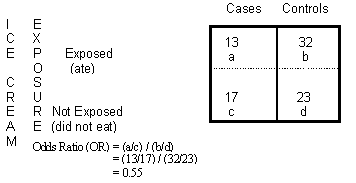



Odds Ratio Calculation And Interpretation Statistics How To
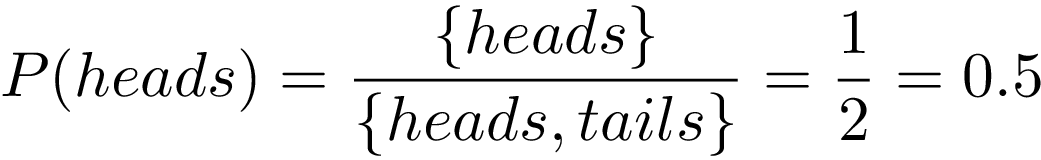



Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science



Q Tbn And9gctxz8owky Sul84xtk4ggzacxwhkmhguhlxwyjj9avufagdrhwm Usqp Cau




How To Calculate Odds 11 Steps With Pictures Wikihow




How To Calculate Odds 11 Steps With Pictures Wikihow



Faq How Do I Interpret Odds Ratios In Logistic Regression




Binary Logistic Regression With Odds Ratios Calculated For The Download Table



Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1




Odds Ratio Wikipedia



Q Tbn And9gctxz8owky Sul84xtk4ggzacxwhkmhguhlxwyjj9avufagdrhwm Usqp Cau



1




Probability Vs Odds Youtube




How To Read And Calculate Sports Odds Everything You Need To Know Betting 101




E Birbeck 7 04 Simple Probability Definition Probability The Chance Some Event Will Happen It Is The Ratio Of The Number Of Ways Ppt Download




Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios
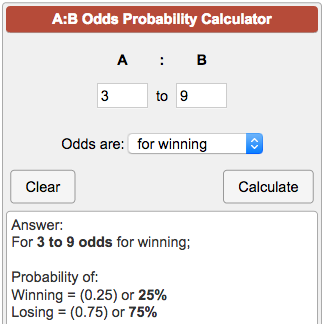



Odds Probability Calculator



The Odds Of Becoming A Millionaire



Statistics Of Dice Throw




Classification Methods And Assessment




Probability Vs Odds In Favour Or Against An Event Examples Youtube




Odds Ratio Hazard Ratio And Relative Ratio Hazard Ratio And Relative Risk 63 Table 5 Examples Of Rr And Or For Different Probabilities ˇ 1 ˇ 2 Rr Or 4 1 4 6 2 3 67 58 04 Pdf Document
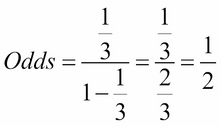



Probability Odds And Log Odds Principles Of Data Science




Statistics 12 Probability Vs Odds Stats Seandolinar Com




Probability Odds And Random Chance Gambling Gaming Technology Use



Ctspedia Ctspedia Oddsterm




What Are The Chances Scientific American




Bayes Rule Odds Form Intro Math 1




Maximum Likelihood Estimate And Logistic Regression Simplified Pavan Mirla
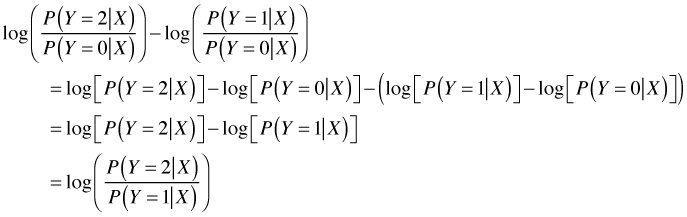



Lecture 38 Monday April 16 12




Odds Ratio Relative Risk
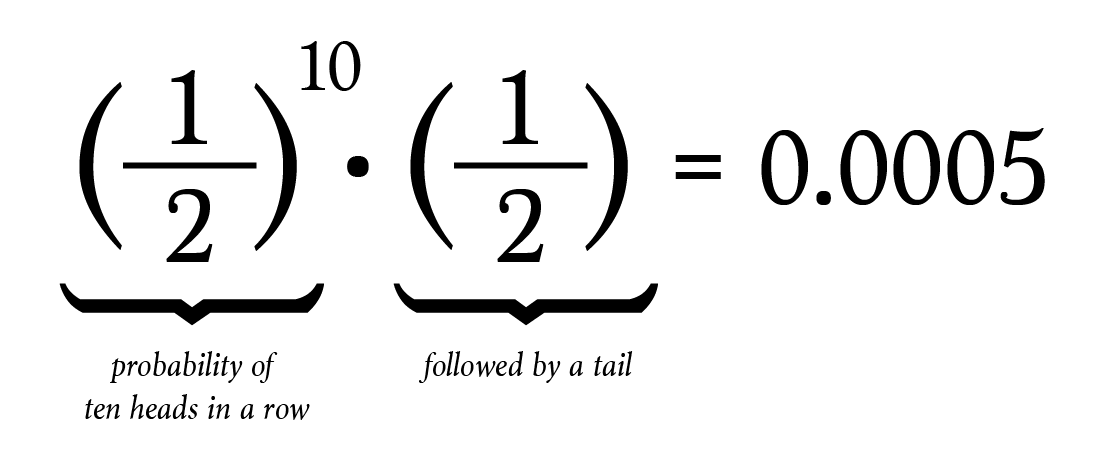



That Common Misconception About Probability By Brett Berry Math Hacks Medium
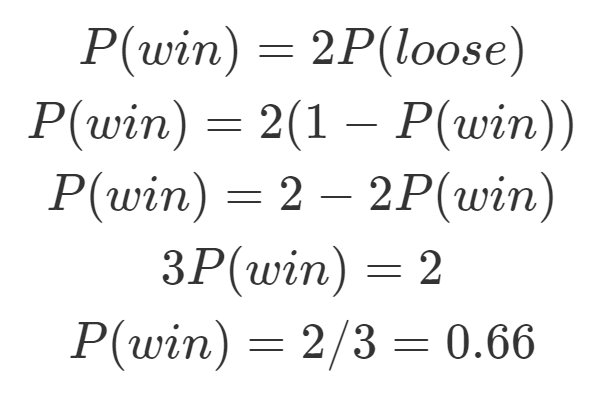



Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science
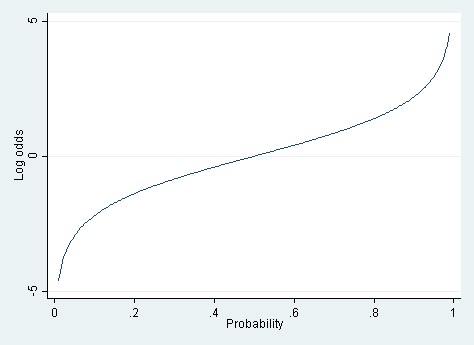



Linear Vs Logistic Probability Models Which Is Better And When Statistical Horizons




Estimates Of Odds Ratios Of Daily Probability Of Diarrhea In The Download Scientific Diagram




Simple Probability Definition Probability The Chance Some Event




Binary Logistic Regression With Odds Ratios Calculated For The Download Table



Odds Likelihood Ratios Guide To Diagnostic Tests




Chapter 6 Choosing Effect Measures And Computing Estimates Of Effect Cochrane Training




How To Read And Calculate Sports Odds Everything You Need To Know Betting 101




Odds Wikipedia




Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1



Are You Mixing Up Odds With Probability By Keith Mcnulty Towards Data Science



Logistic Regression
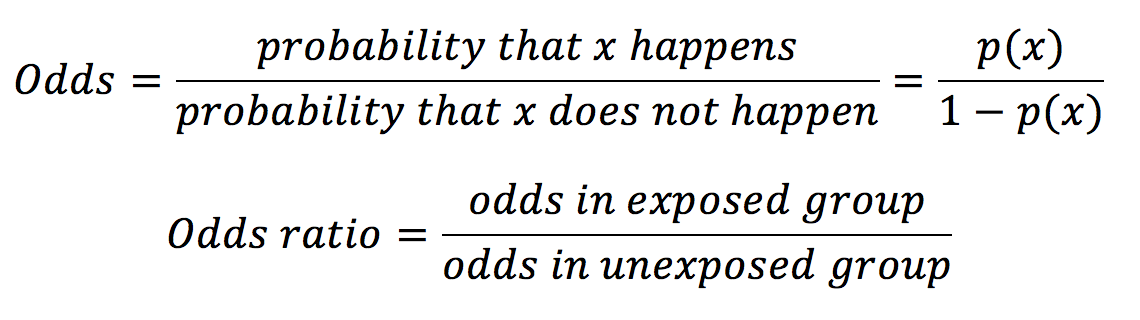



Statistics For Medical Students Geeky Medics




Converting Probability To Odds Example Youtube




Statquest Odds And Log Odds Clearly Explained Youtube



0 件のコメント:
コメントを投稿